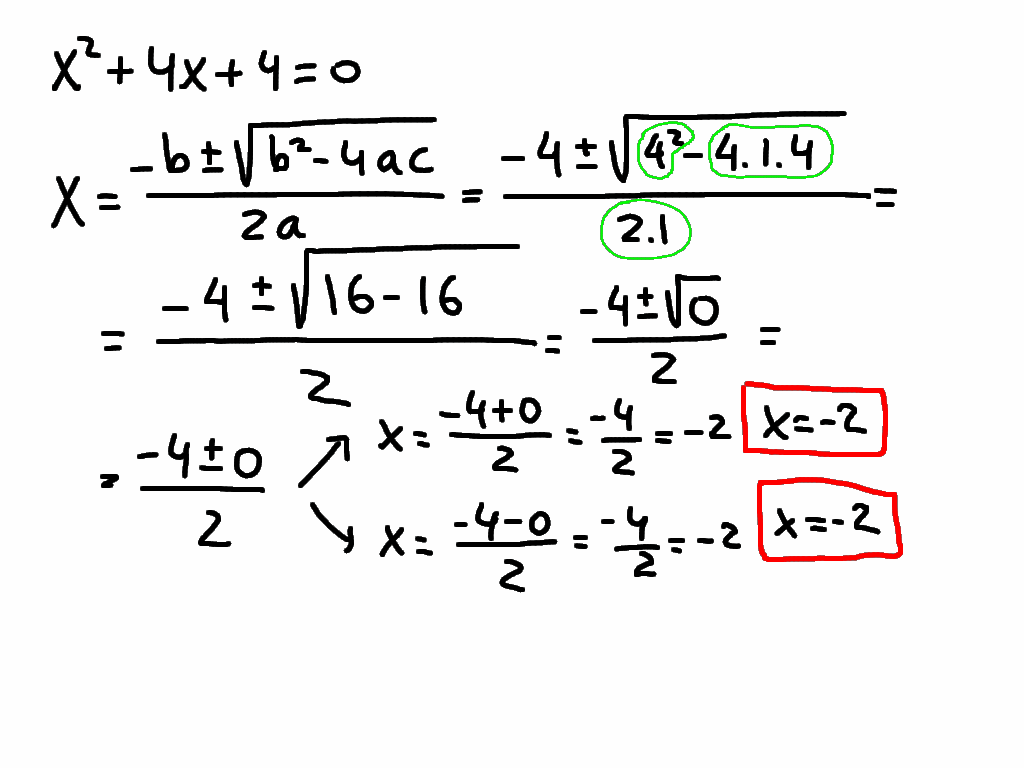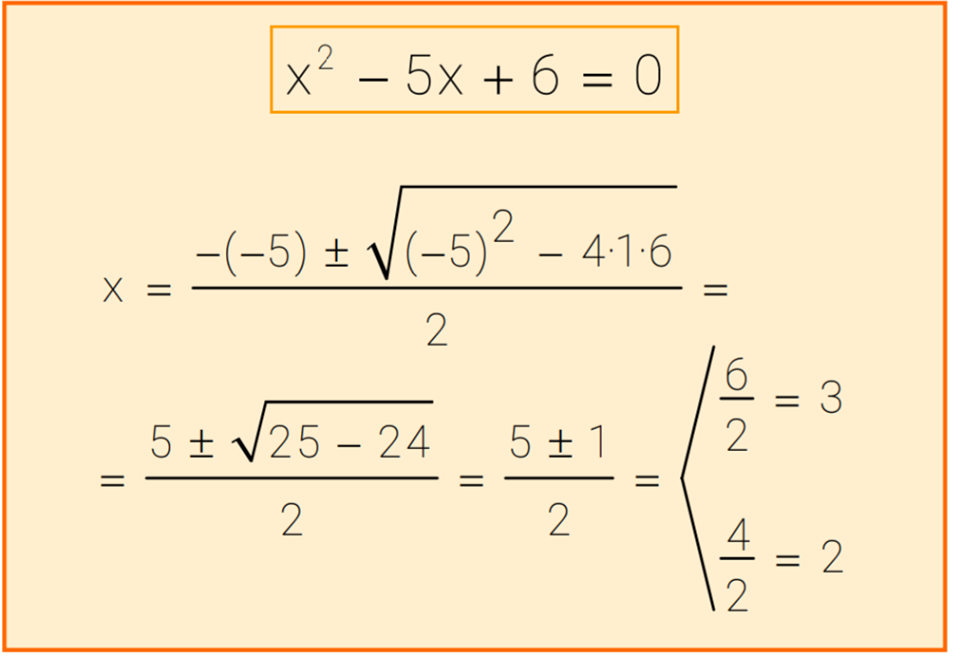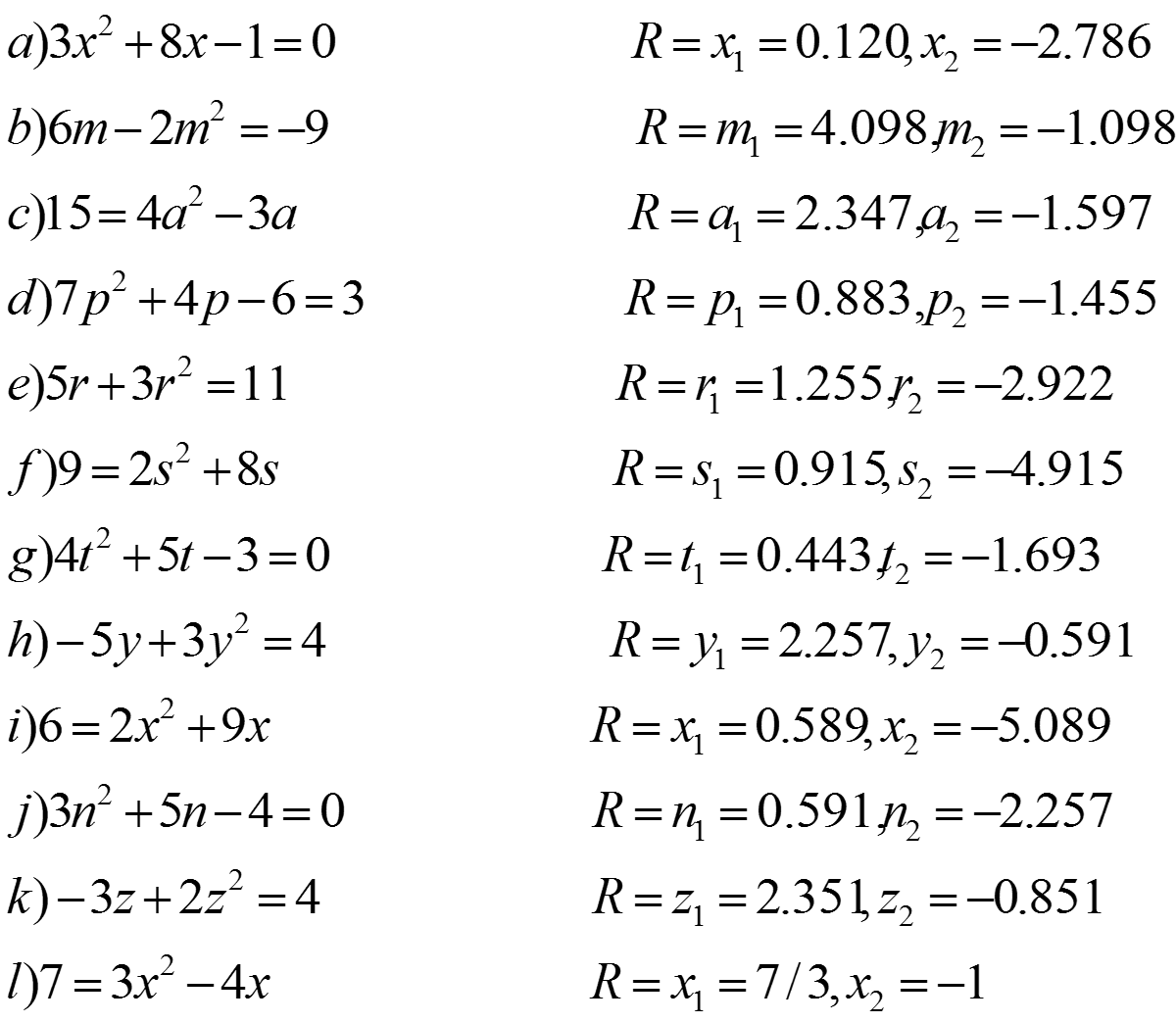Unraveling the Power of Quadratic Equations
Imagine throwing a ball into the air. Can you predict its path? This act, seemingly simple, hides a complex mathematical dance: the trajectory of a projectile, a phenomenon governed by what we call quadratic equations.
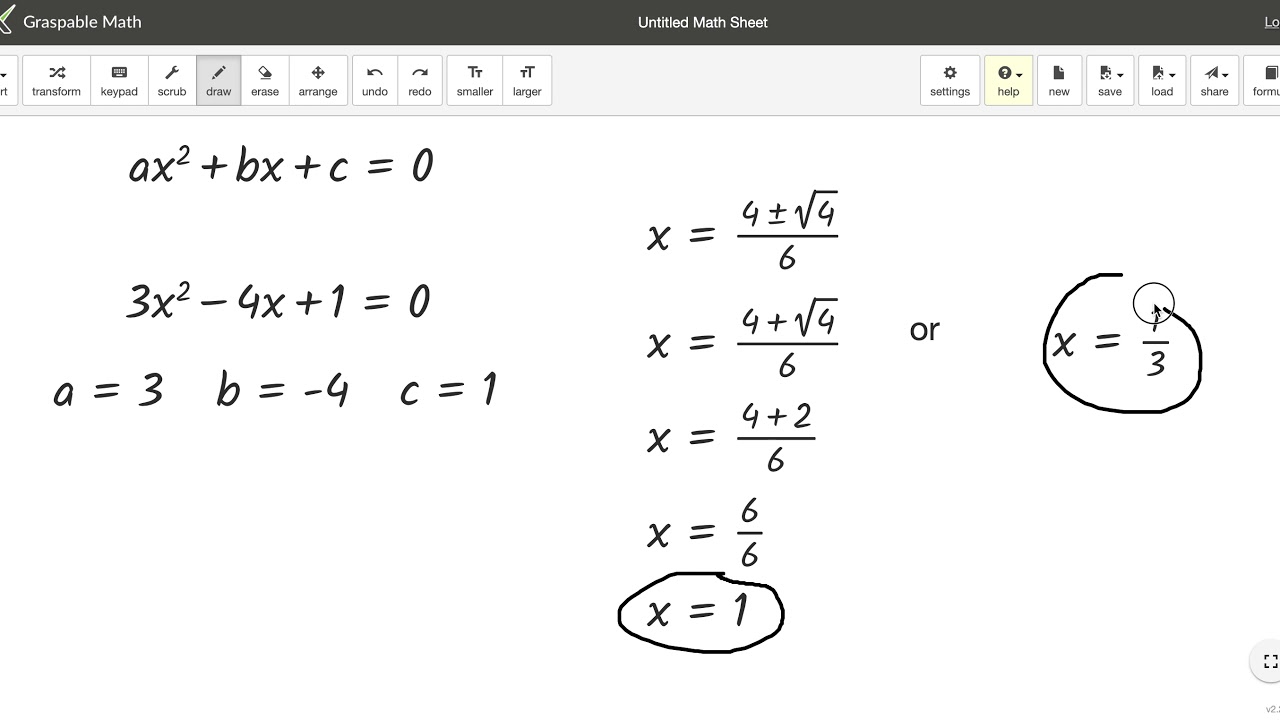
Quadratic equations, expressions with a highest power of two, are more than just abstract formulas confined to textbooks. They are the secret language the universe uses to describe parabolic paths, analyze the motion of objects under gravity, and even design the lenses in your camera.
From the elegant curves of suspension bridges to the precise calculations behind financial models, these equations are powerful tools with applications across diverse fields. Understanding their structure and solutions unlocks a deeper understanding of the world around us.
The journey of quadratic equations began centuries ago, with early mathematicians grappling with problems involving areas and lengths. Babylonians, known for their advanced mathematical knowledge, developed algorithms to solve these equations, primarily for land surveying and inheritance distribution.
The baton was then passed on to the Greeks, with Euclid and Diophantus contributing significantly to the development of geometric and algebraic solutions, respectively. Over the centuries, mathematicians like Brahmagupta in India and al-Khwarizmi in Persia further refined these methods, shaping our understanding of quadratic equations into what it is today.
Advantages and Disadvantages of Quadratic Equations
| Advantages | Disadvantages |
|---|---|
| Provide precise solutions for complex problems | Can be challenging to solve for beginners |
| Applicable in numerous fields, including physics, engineering, and finance | May not always reflect real-world scenarios perfectly due to simplifying assumptions |
Let's delve deeper into the practical applications of quadratic equations. Imagine you're an engineer designing a bridge. You need to calculate the exact curve of the cables to ensure the bridge can withstand the weight of vehicles. Quadratic equations provide the mathematical framework for this calculation, ensuring the bridge's stability and safety.
Or perhaps you're a physicist studying the motion of a rocket launched into space. By using quadratic equations, you can model the rocket's trajectory, predict its maximum height, and determine the time it takes to reach its destination. The ability to model and predict such complex movements is invaluable in fields like aerospace engineering and astronomy.
Even in the realm of finance, quadratic equations play a crucial role. Financial analysts use these equations to model market trends, predict stock prices, and manage investment portfolios. By understanding the behavior of quadratic functions, they can make more informed financial decisions.
While quadratic equations offer a powerful tool for solving a wide range of problems, it's important to acknowledge that mastering them requires practice and a solid understanding of mathematical concepts. However, the ability to apply these equations opens doors to a deeper understanding of the world and empowers us to tackle complex challenges across various disciplines.
Protecting your little one a guide to hyperlite infant life jackets
Navigating together understanding llcs for husband and wife businesses
The power of philippine speeches shaping the nations narrative